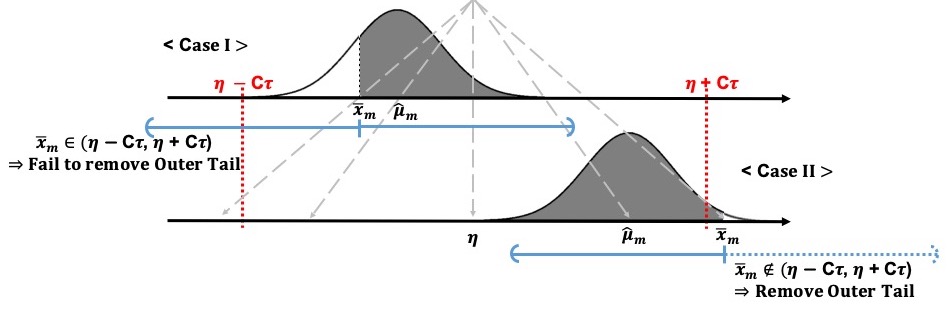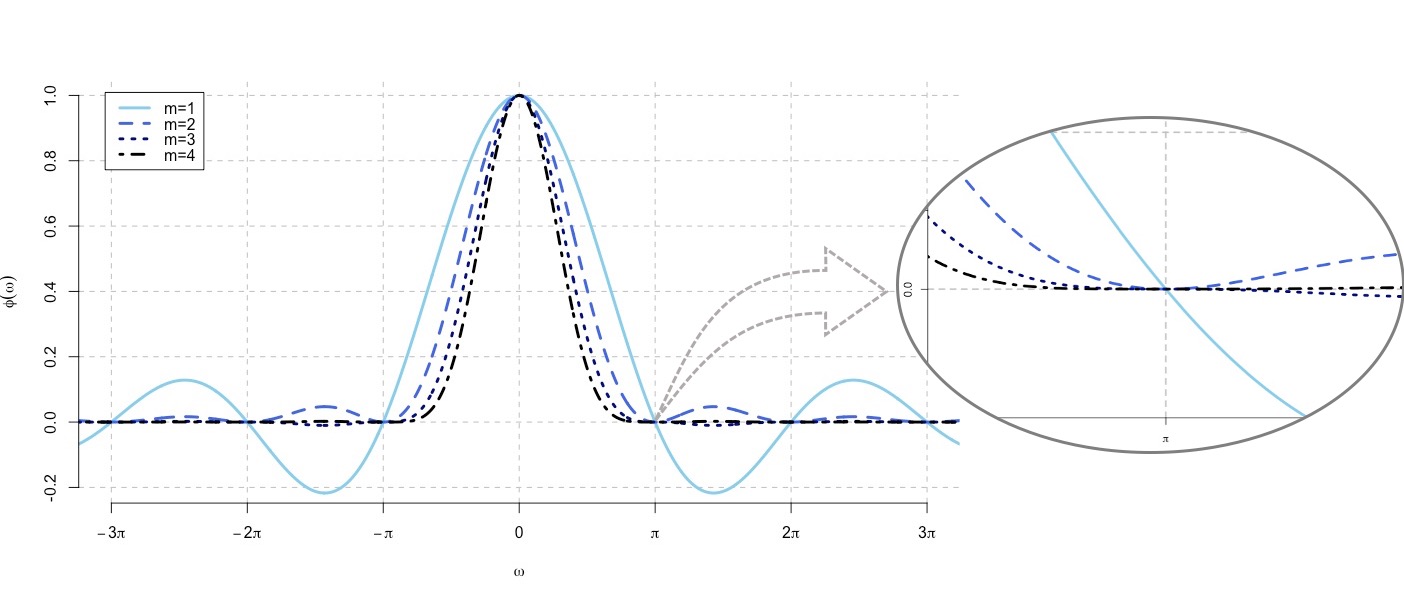
It is a conventional assumption in density deconvolution problems such that the characteristic function of the measurement error distribution is non-zeros on the real line. However, there are many instances of problems in which the assumption is violated, for example, with the convolution of uniform distribution in the figure. Goldenshluger and Kim (2021) investigate the problem with the non-standard error distributions -- namely, that their characteristic functions have zeros on the real line -- by ascertaining how the multiplicity of the zeros affects the estimation accuracy. For this investigation, we develop optimal minimax estimators and derive the corresponding lower bounds. From that result, the best achievable estimation accuracy is determined through the multiplicity of zeros, the rate of decay of the error characteristic function, and the smoothness and tail behavior of the estimated density. In addition, we consider the problem of adaptive estimation by proposing a data-driven estimator that automatically adapts to the unknown smoothness and tail behavior of the density to be estimated.

In this work, a thresholding approach for an MIE is utilized, with the goal of removing one side from some interval estimators (IEs) in order to minimize the global expected length. To set up the thresholds, the prior distribution, e.g., the normal-normal model, is adopted. The thresholding procedure then removes the outer-tails for the IEs, in cases where the corresponding point estimates fall far from the prior mean. This process could be justified by observing the likelihoods (the grey areas in the figure) that the parameters fall within the inner-tails. In cases where a higher likelihood exists (as in case II), the outer tail should ideally be removed, since it does contribute to the coverage probability; on the other hand, when there is a lower likelihood, it is better to maintain the outer-tail (case I). In Kim and Peña (2019), we illustrate the performance of MIEs with thresholding through simulations and applications to in-season batting average and leukemia gene expression data. The results suggest that the thresholding procedure provides considerable reductions in the global expected length while satisfying the global coverage rate requirement. The procedure has also been studied for the exponential-inverse gamma, and holds great potential for application to other conjugate families.

This study came in response to the current pandemic and attempts to construct prediction intervals (PIs) for the daily and cumulative COVID-19 deaths in the U.S. To handle the observed over-dispersion in the data, Kim et al. (2020) introduce a novel approach, called a frailty-based procedure, combining it with the Poisson regression model. While the PIs perform well for relatively short-term prediction, e.g., 10- to 30-day windows, they start to become overly conservative for wider prediction windows, reflecting not only the limitations of the procedure, but also the inherent difficulties of forecasting on a long horizon. In another review paper, Kim et al. (2021) further explore PI problems based on Poisson regression results. In that manuscript, we thoroughly review various PI procedures for the Poisson regressions with no covariates, standard Poisson regressions, and Poisson regressions that respond to the over-dispersion issue.